Identificación de Colmenas Salvajes mediante Triangulación
Un proyecto científico colaborativo para localizar y estudiar colmenas silvestres en Puerto Rico
¿Qué es la triangulación?
La triangulación en este proyecto es una técnica utilizada para estimar la ubicación de colmenas silvestres observando el comportamiento de vuelo de las abejas desde tres puntos diferentes donde se colocan alimentadores artificiales. Desde cada uno de estos puntos, se mide el ángulo en el que la abeja se aleja al regresar a su colmena.
¡Dato interesante!
Las abejas obreras tienen la costumbre de volver en línea recta a su colmena desde la zona de alimentación, proporcionando así una dirección más precisa tras múltiples vuelos de idea y vuelta (Brown, 2010).
Al registrar los ángulos desde las tres posiciones, se trazan líneas que representan la dirección promedio del vuelo de la abeja desde cada punto, este promedio calculado con estadística circular para evitar errores (por ejemplo, 359° y 1° están muy cerca, pero un promedio lineal daría un valor erróneo). Luego se trazan líneas que representan dos desviaciones estándar circulares que indican la variabilidad en las trayectorias, definiendo así un área probable de vuelo. Finalmente, la intersección de las áreas trazadas de cada una de las abejas permitirá estimar la ubicación más probable de la o las colmenas salvajes alrededor de las escuelas.
En resumen, la triangulación en este contexto consiste en usar las direcciones de vuelo registradas de abejas identificadas desde tres ubicaciones para trazar líneas que se intersectan en la posible ubicación de la colmena silvestre, apoyándose en la precisión del vuelo en línea recta de las abejas y en análisis estadísticos circulares para definir un área de mayor probabilidad.
Georreferenciación
La georreferenciación es el uso de coordenadas de mapa para asignar una ubicación espacial a entidades cartográficas (Esri, s.f.). En nuestro proyecto, esta técnica es fundamental para establecer puntos de referencia precisos.
¿Por qué es esencial la georeferenciación en la triangulación?
Determinamos las coordenadas reales exactas de cada alimentador, ubicado en tres posiciones diferentes en el área donde realizamos el BeeHunting. Esto nos permite:
- Establecer puntos de referencia precisos para las mediciones
- Crear mapas exactos de las ubicaciones de las colmenas
- Compartir datos con otros investigadores de manera consistente
- Realizar análisis espaciales avanzados
Un ejemplo de la georreferenciación, se dio en la Escuela Pedro Falú Orellano, en la que gracias a la georreferenciación obtuvimos las siguientes coordenadas del alimentador artificial en tres posiciones diferentes:
| Posición del alimentador | Longitud (Eje X) | Latitud (Eje Y) |
|---|---|---|
| Primera posición | 262968.6995 m | 260675.0443 m |
| Segunda posición | 262982.7388 m | 260661.3309 m |
| Tercera posición | 262993.5497 m | 260675.4780 m |
Estas coordenadas son fundamentales para colocar la media y las desviaciones estándar circulares tanto en papel como en software especializado.
Triangulación en papel
Materiales requeridos:
- Papel cuadriculado
-
 Transportador
Transportador
- Compás
- Regla
- Lápiz
- Goma
Procedimiento detallado
Colocar las coordenadas en el papel cuadriculado
Como se pudo ver en el ejemplo, las coordenadas (latitud y longitud) de los alimentadores son valores a gran escala, por lo que para dibujar en un papel cuadriculado, se hará un ajuste a las coordenadas de manera que sea más sencillo colocarlo en el papel.
Procedimiento detallado:
- Ajuste de coordenadas
- Longitud mínima (X): 262968.6995 m
- Latitud mínima (Y): 260661.3309 m
- Reducción de escala
Primero, identificamos el valor más pequeño de latitud y el valor más pequeño de longitud en la tabla. Luego, restamos esos valores a cada uno de los datos correspondientes. Este procedimiento se llama traslación, y no cambia la forma ni la proporción entre los puntos.
Ejemplo con coordenadas reajustadas
Coordenadas trasladadas de los alimentadores
| Posición del alimentador | Longitud (Eje X) | Latitud (Eje Y) |
|---|---|---|
| Primera posición | 0.0000 m | 13.7134 m |
| Segunda posición | 14.0393 m | 0.0000 m |
| Tercera posición | 24.8502 m | 14.1471 m |
Después de trasladar las coordenadas de los alimentadores, se realiza una reducción de escala dividiendo cada valor entre 10. Esto permite trabajar con números más pequeños y facilita el dibujo en el papel cuadriculado. Este procedimiento en matemática también se llama dilatación o transformación de homotecia.
Coordenadas dilatadas de los alimentadores
| Posición del alimentador | Longitud (Eje X) | Latitud (Eje Y) |
|---|---|---|
| Primera posición | 0.0000 m | 1.37134 m |
| Segunda posición | 1.40393 m | 0.0000 m |
| Tercera posición | 2.48502 m | 1.41471 m |
En las siguiente imagen se puede observar que al realizar las tranformaciones anteriores la proporción de las localizaciones se mantienen.
Puntos originales de los alimentadores
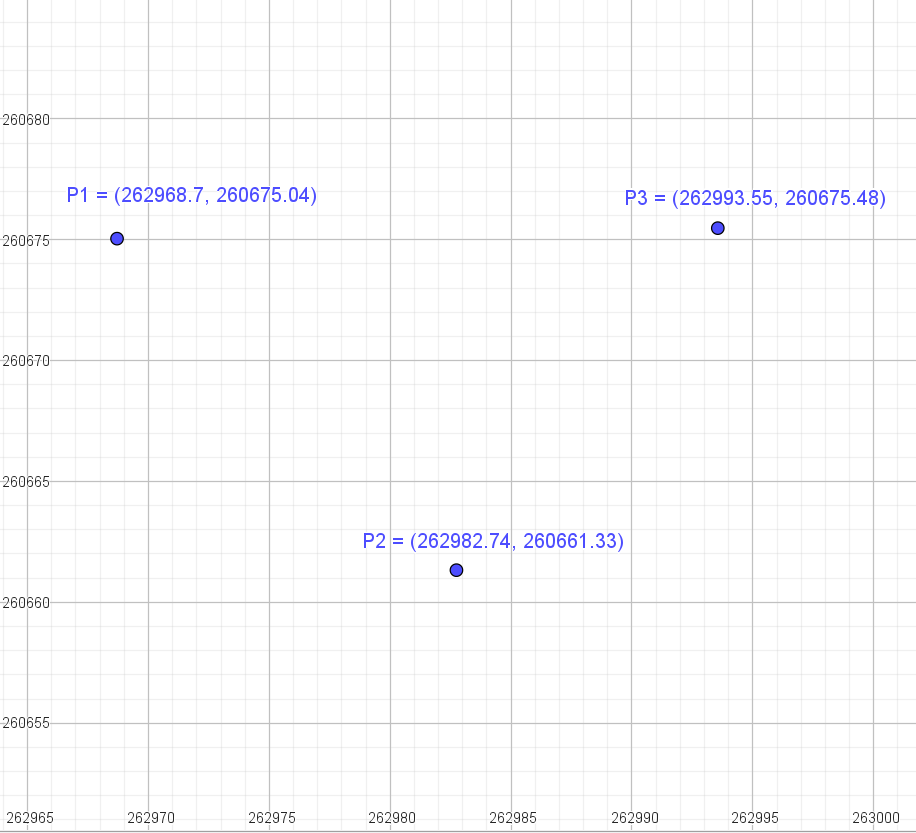
Puntos al realizar la traslación y la dilatación
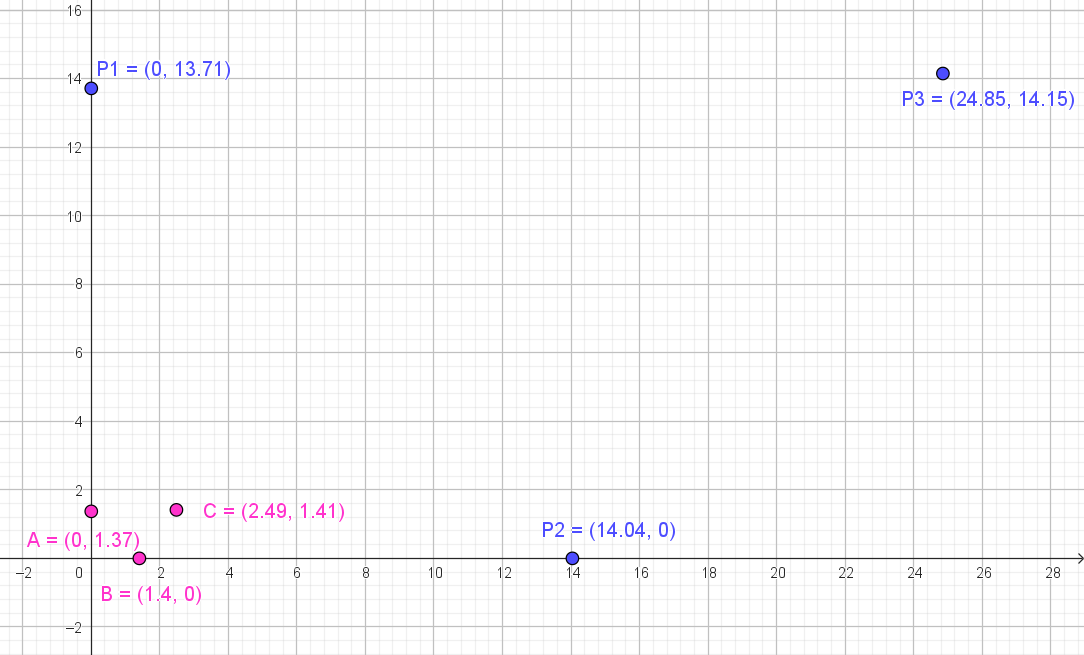
Preparación del plano cartesiano para el trazado de ángulos
En esta sección prepararás el plano donde se representarán las trayectorias de vuelo de las abejas desde cada alimentador, utilizando los ángulos obtenidos durante la observación.
Procedimiento detallado:
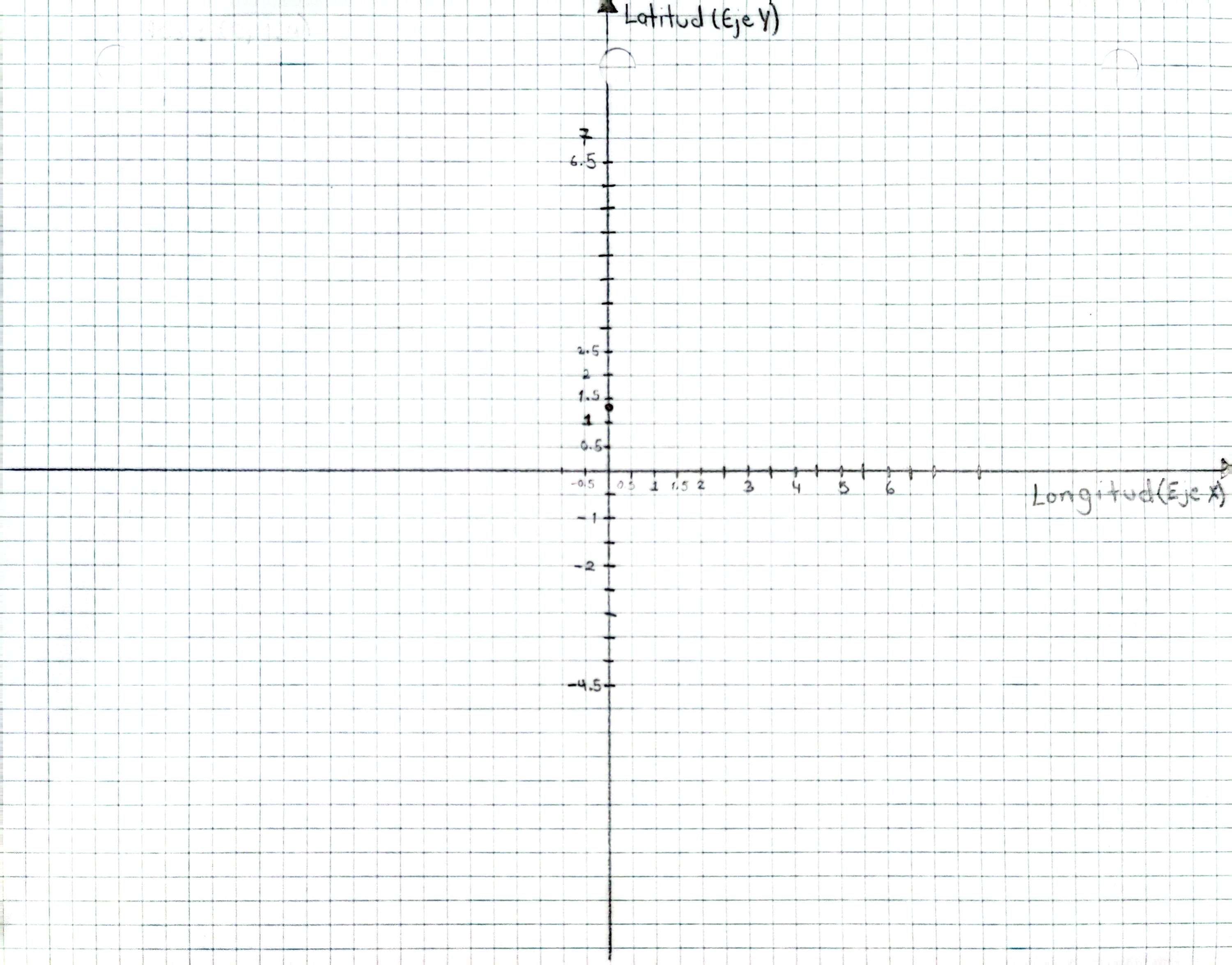
- Dibuja un plano cartesiano en papel cuadriculado que incluya los cuatro cuadrantes. Establece una escala clara (por ejemplo, cada cuadrito equivale a 0.5 unidades en los ejes X e Y) o ajústala según tus necesidades. Puedes tomar como guía la siguiente imagen:
- Ubica las coordenadas de cada alimentador según los datos obtenidos en el Paso 1 y la escala elegida.
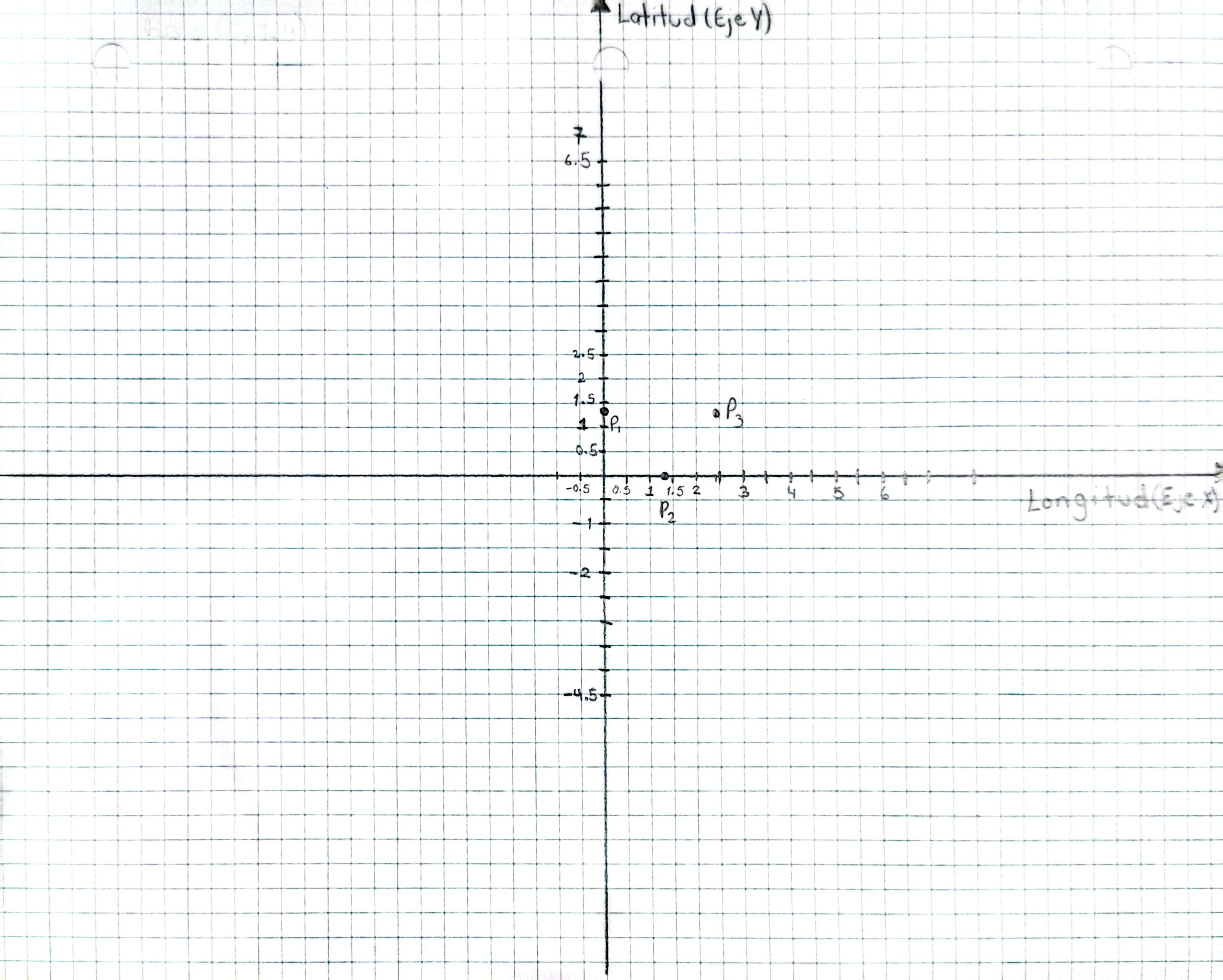
- Marca claramente cada punto de alimentación con su nombre (P1, P2, P3). Puede usar diferentes colores para facilitar la identificación.
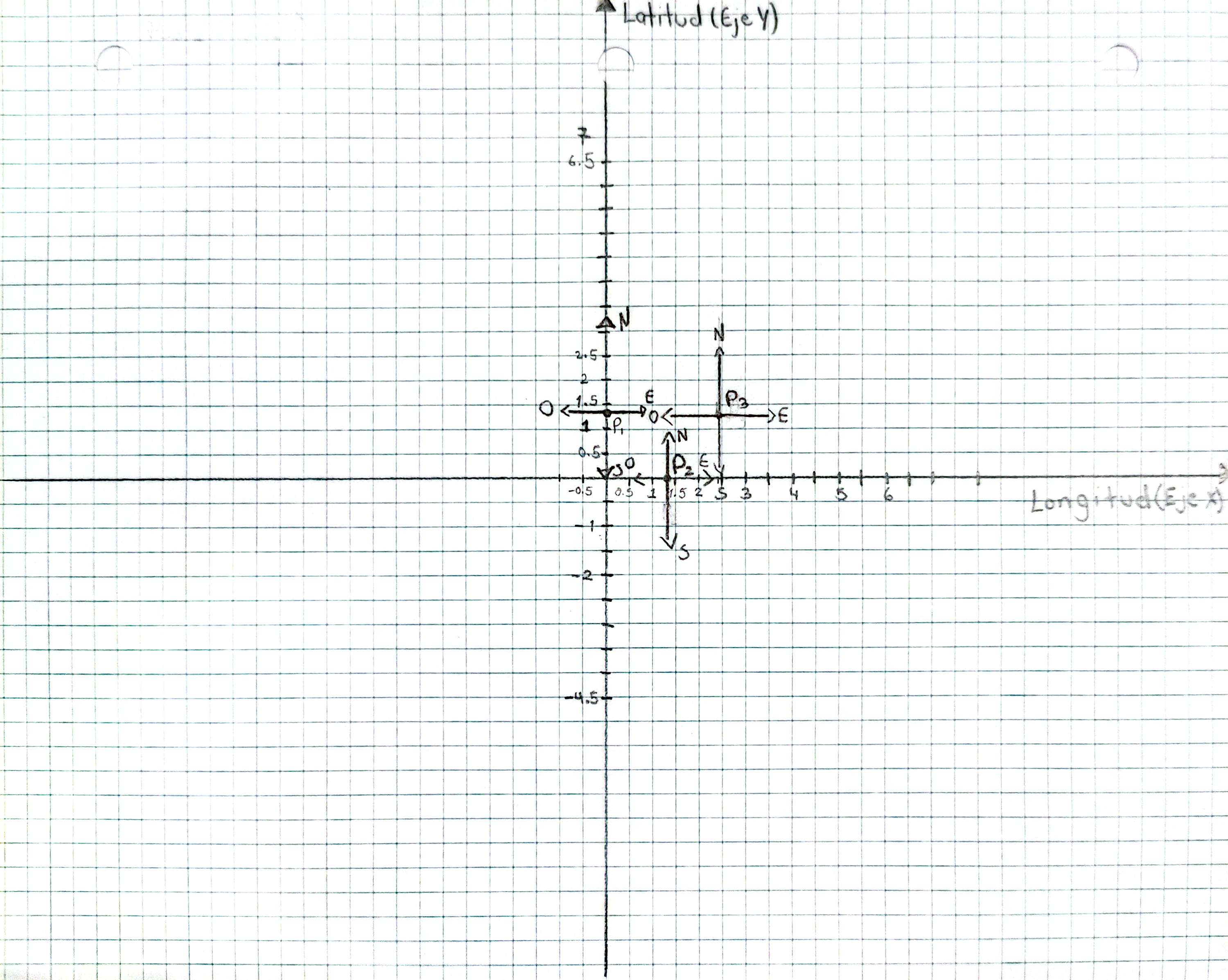
- En cada punto marcado (P1, P2 y P3), traza dos líneas guía: una línea horizontal (paralela al eje X) y una vertical (paralela al eje Y), formando una cruz. Estas líneas representan los puntos cardinales: norte (arriba), sur (abajo), este (derecha) y oeste (izquierda). Esta referencia facilitará el trazado de los ángulos.
Los dos pasos anteriores se ilustran en la siguiente imagen:
Trazado de la media circular y rango de desviación
Una vez preparados los puntos de referencia, se procede a representar gráficamente el ángulo promedio (media circular) del vuelo de cada abeja desde cada punto de alimentación, así como la desviación circular que indica el posible rango de dirección.
Procedimiento:
- Coloca el centro del transportador sobre cada punto de alimentación (P1, P2 y P3).
- Alinea el transportador con el norte (0°), representado por la línea vertical hacia arriba en cada punto (P1, P2 y P3). Recuerda que los ángulos se miden en el sentido de las agujas del reloj.
- Utiliza los valores de la media circular obtenidos para cada punto para marcar la dirección promedio del vuelo de la abeja:
- P1: 201.34°
- P2: 232.12°
- P3: 240.31°
- Desde cada punto, marca también un rango que represente dos desviaciones estándar a cada lado del ángulo promedio. Por ejemplo:
- P1: ±25.52°
- P2: ±17.18°
- P3: ±16.48°
- Traza tres rayos desde cada punto:
- Un rayo en la dirección exacta del ángulo promedio (media circular).
- Dos rayos punteadas adicionales que marquen el límite superior e inferior del rango de variación (ángulo promedio ± desviación).
- Estas líneas formarán un sector que representa el rango probable en el que la abeja voló hacia su colmena. Puedes sombrear suavemente esa área si deseas destacarla como en la siguiente imagen:
- Puede pintarse las áreas de la siguiente manera
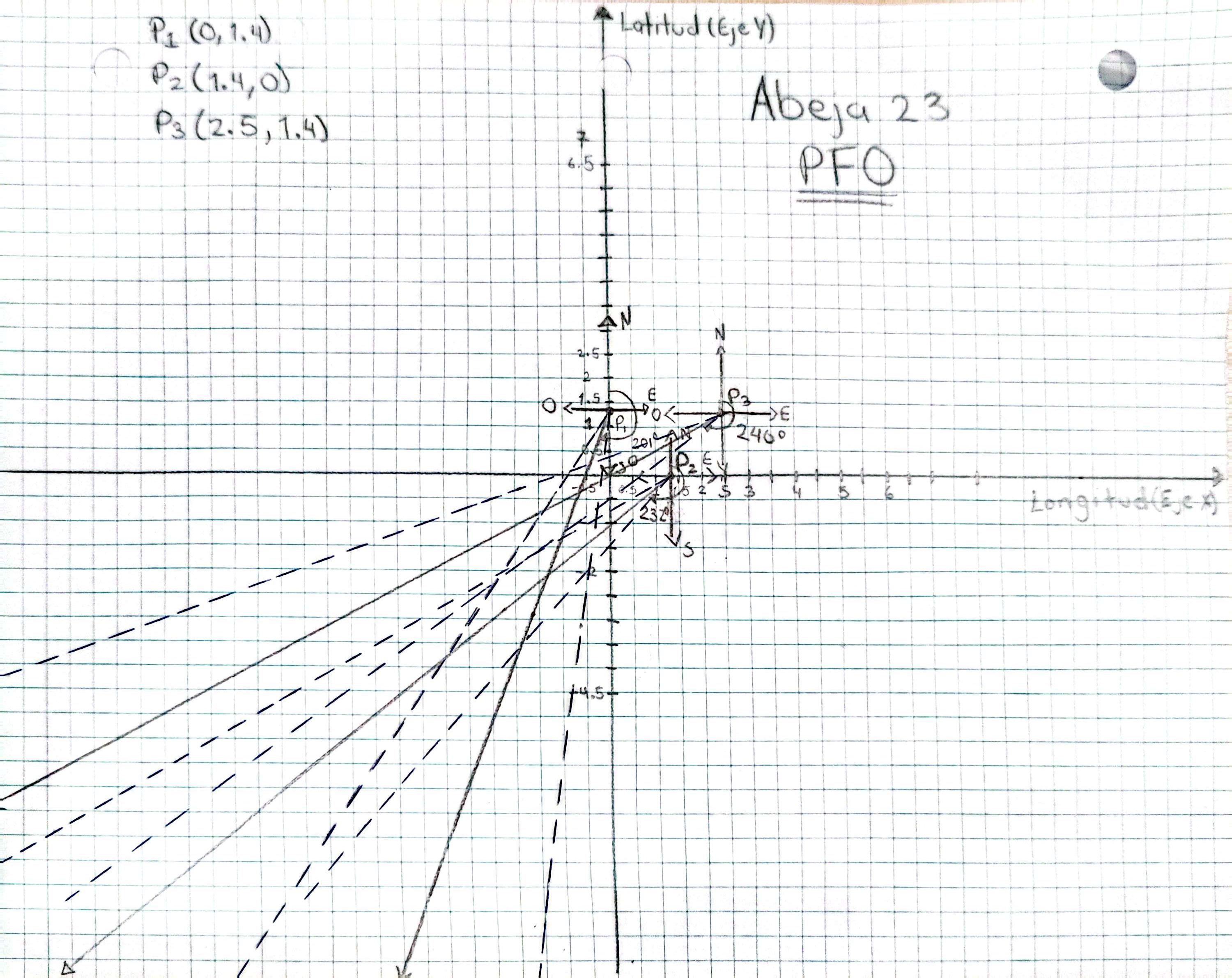
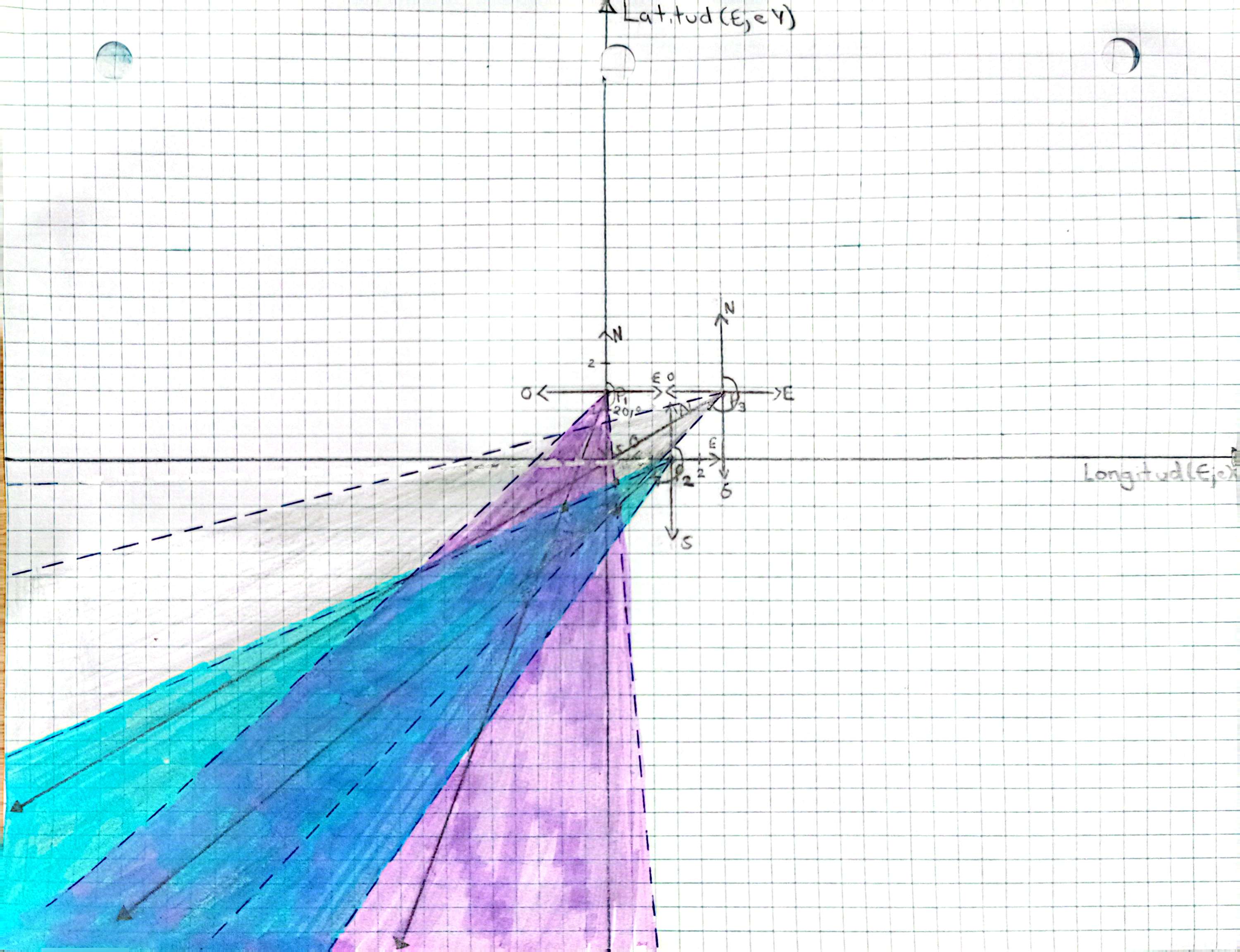
Identificar el área de intersección
Localiza la zona donde se cruzan las líneas trazadas desde los tres puntos para determinar la ubicación probable de la colmena.
Procedimiento detallado:
- Observa el punto donde se cruzan las tres líneas principales (triangulación perfecta)
- Si no hay un punto exacto de intersección (debido a variaciones naturales), identifica el área triangular donde las líneas se aproximan más
- Marca esta área como la posible ubicación de la colmena
- Considera la variabilidad estadística trazando un margen de error de ±2 desviaciones estándar a cada lado de la línea principal
- Dibuja un círculo o polígono que represente la zona probable de la colmena basado en estas intersecciones
Precisión: La intersección de las tres líneas indica la ubicación más probable de la colmena. El área de intersección de las zonas de desviación estándar representa el margen de error de nuestra estimación.
Triangulación con GeoGebra
GeoGebra es un software matemático interactivo que permite realizar el proceso de triangulación con mayor precisión. Sigue los siguientes pasos para aprender a usar GeoGebra y a la vez realizar la triangulación:
Ingresar puntos de ubicación de los alimentadores:
Introduce las coordenadas de los tres puntos de alimentación en GeoGebra:
Procedimiento detallado con un ejemplo:
- En el campo de entrada (Input), escribe las coordenadas:
(0, 1.37134)y presiona Enter - Ingresa el segundo punto:
(1.40393, 0) - Ingresa el tercer punto:
(2.48502, 1.41471) - Renombra los puntos como P1, P2 y P3 respectivamente. Da clic derecho sobre cada punto y selecciona "Rename", borra el nombre del punto y coloca P1, P2 o P3 según corresponda.

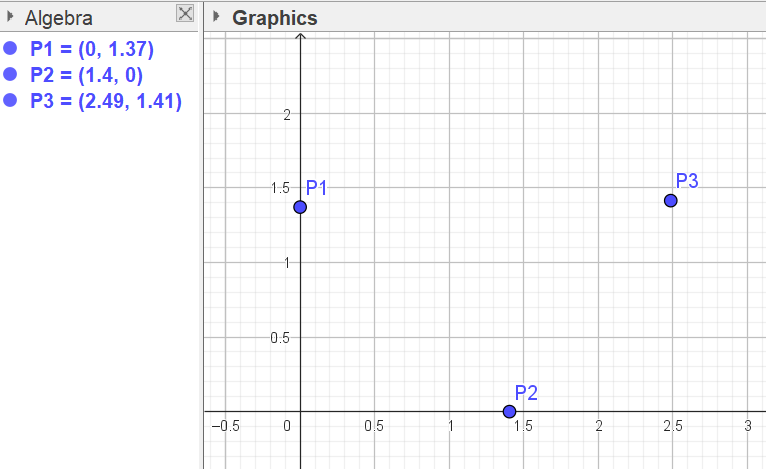
Construir líneas y ángulos
Prepara el espacio para medir los ángulos de dirección:
Procedimiento detallado:
- Traza tres rectas paralelas al eje Y que pasen por cada punto (P1, P2, P3)
- Coloca un punto adicional sobre cada recta (por encima de P1, P2 y P3)
- Usa la herramienta "Angle with given size" (Ángulo con tamaño dado)
- Selecciona primero el punto adicional y luego P1
- Ingresa el ángulo en grados y selecciona "Clockwise" (sentido horario) y da clic sobre OK
- Repite para P2 y P3 con sus respectivos ángulos
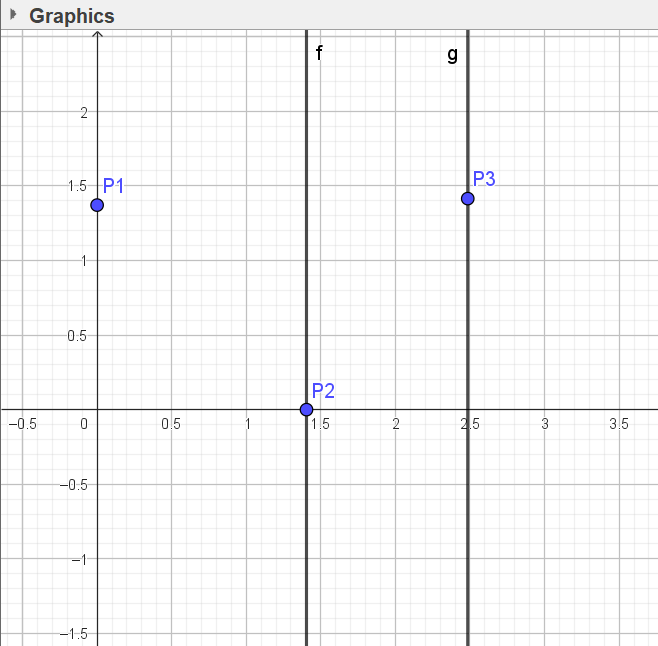
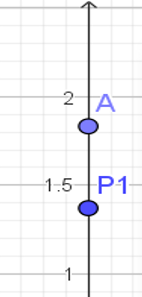
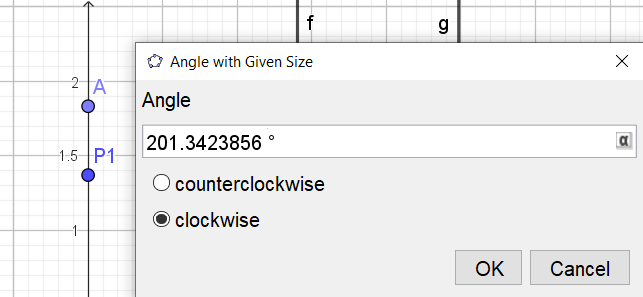
Nota: Asegúrate de usar el símbolo de grados (°) al ingresar los ángulos.
Trazar rayos de dirección
Crea los rayos que representan la dirección del vuelo de las abejas:
Procedimiento detallado:
- Selecciona la herramienta "Ray" (Rayo)
- Para cada punto (P1, P2, P3), traza un rayo desde el punto del alimentador hasta el punto creado automáticamente por la herramienta de creación del ángulo
- Repite el proceso para cada alimentador
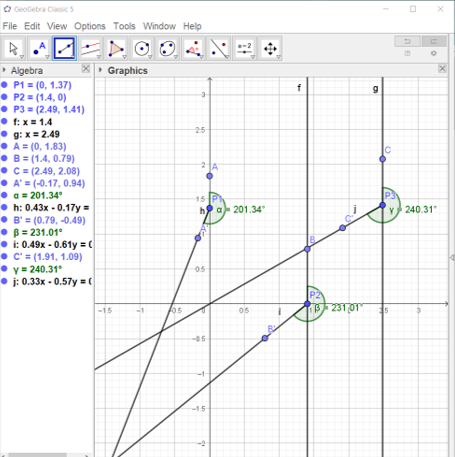
Precisión: Extiende los rayos lo suficiente para asegurar que se crucen.
Analizar intersecciones
Determina la ubicación de la colmena y las áreas de probabilidad:
Procedimiento detallado:
- Para considerar la desviación estándar:
- Usa nuevamente "Angle with given size"
- Para P1: (ángulo original + 2 × desviación estándar)
- Para P1: (ángulo original - 2 × desviación estándar)
- Repite para P2 y P3
- Traza rayos para estas nuevas direcciones y configúralos como punteados
- Identifica el área de intersección de las zonas delimitadas
- Sombree las áreas de cada abeja

Optimización: Oculta los valores innecesarios para una visualización más clara.
Galería del Proyecto de Triangulación
Fotos de las maestras aprendiendo el proceso de traingulación en papel en el verano de 2025